تحليل الانحدار ….Regression Analysis

ناقشت في المقالتين السابقتين كيفية دراسة العلاقة بين متغيرين باستخدام الرسم البياني (المنحنى التنقيطي) Scatter Diagram وكيفية دراسة قوة العلاقة الخطية بين متغيرين باستخدام معامل الارتباط Correlation. في هذه المقالة نناقش كيفية تحديد العلاقة بين متغيرين أو أكثر بشكل أكثر تحديدا وبحيث نستطيع تكوين نموذجا رياضيا لتلك العلاقة. هذا الموضوع هو من الأدوات الرائعة لتحليل البيانات والتي يحتاجها الكثير من الناس.

الانحدار Regression:

تحليل الانحدار   Regression Analysis هو تحليل يمكننا من إيجاد معادلة رياضية تربط بين متغير تابع ومتغير أو متغيرات مستقلة. فمثلا يمكننا باستخدام تحليل الانحدار دراسة العوامل التي تؤثر في زيادة الطلب على المنتج وتحديد نموذجا (معادلة) رياضيا لهذه العلاقة. هذا النموذج يجعلنا قادرين ليس فقط على فهم طبيعة العلاقة وتحديد العوامل المؤثرة فعلا بل إنه يجعلنا قادرين على توقع تأثير تغير أي متغير من هذه المتغيرات المستقلة على المتغير التابع.

الحاجة لاستخدام هذا الانحدار كثيرة ومتنوعة. فالمهندس يحتاج لدراسة العوامل التي تؤثر في ارتفاع درجة حرارة الغازات المستخدمة في عملية ما وقد يكون لديه العديد من العوامل التي يريد أن يعرف تأثيرها الحقيقي. باستخدام الانحدار فإن هذا المهندس يستطيع تحديد العوامل المؤثرة وإهمال تلك غير المؤثرة ويمكنه توقع التغير الذي يحدث في درجة حرارة الغازات نتيجة لتغير محدد في أي من تلك المتغيرات المؤثرة. ومدير الموارد البشرية يريد تحديد العوامل التي تؤثر على أداء العاملين الجدد من بين عدة عوامل مثل السن وتقدير التخرج وجامعة الدراسة وغيرها. فيمكنه باستخدام تحليل الانحدار معرفة ما هي العوامل التي لا تؤثر ولا ترتبط بأداء العاملين الجدد وتلك المؤثرة ويمكنه الحصول على نموذجا رياضيا يمكنه من توقع وفهم حجم تأثير تلك العوامل على الأداء.

ماهو الحل البديل لتحليل الانحدار؟ إنه محاولة تغيير أحد العوامل مع تثبيت العوامل الأخرى ثم إجراء ذلك مع كل عامل من العوامل الأخرى وهذا غير متاح في الواقع العملي . فلا يمكنك أن تطلب من درجة حرارة الجو أن تثبت حتى تدرس تأثير تأثير نسبة الأتربة في الجو على صحة البشر. وكذلك لا يمكنك أن تقوم بتثبيت سرعة الماكينة في العمل لمدة أسبوع لتدرس تأثير نوع الزيت المستخدم بشكل مستقل عن تغير السرعة. تحليل الانحدار يجعلنا لا نلجأ لهذه الطرق شبه المستحيلة فبمجرد وجود عينة من البيانات للمتغيرات المختلفة يمكننا تحديد العوامل المؤثرة وطبيعة تأثيرها بشكل محدد وواضح.

أنواع تحليل الانحدار: هناك نوعان من تحليل الانحدار أولهما هو الانحدار الخطي وهو الأكثر انتشارا. الانحدار الخطي يعني أننا ندرس العلاقة الخطية. أما النوع الثاني فهو الانحدار غير الخطي والذي نحتاجه عند دراسة علاقات على شكل منحنى وليس خطا مستقيما. الانحدار الخطي هو الأكثر شيوعا وهو الذي نناقشه هنا. والانحدار الخطي له نوعان بسيط ومتعدد فالبسيط يحاول التنبؤ بالعلاقة بين متغير ما وعامل واحد يؤثر فيه والمتعدد يحاول التنبؤ بالعلاقة بين متغير ما وعدة عوامل تؤثر فيه. في هذه المقالة نناقش النوع الأول وهو الانحدار الخطي البسيط.

الانحدار الخطي البسيط Simple Linear Regression

الانحدار الخطي البسيط هو دراسة العلاقة بين متغيرين فقط بحيث نحاول الوصول إلى علاقة خطية (أي معادلة خط مستقيم) بين هذن المتغيرين في صورة:

ص= ث  + أ  x  س

حيث ص و س هما متغيران وث وأ هما ثابتان. هذه المعادلة هي المعادلة التي ترسم خطا مستقينا بين س و ص. لاحظ أن ص هنا يسمى متغيرا تابعا أي أن تغيره يتبع تغير س وأما س قيسمى متغيرا مستقلا أي أن تغيره هو تغير مستقل وهذه تسميات رياضية فقط.

فمثلا نريد أن نعرف طبيعة العلاقة بين متوسط ساعات الدراسة ودرجة الطلبة في الامتحانات أو نريد دراسة العلاقة بين سعر المنتج وحجم المبيعات أو نريد دراسة العلاقة بين عدد المنتجات المعيبة ومعدل التحميل أو نريد دراسة العلاقة بين استهلاك الكهرباء في الساعة ودرجة حرارة الجو.

مثال: قبل أن نستفيض في شرح تحليل الانحدار دعنا نرى كيف يمكننا إجراء مثل هذا التحليل.

افترض أننا سجلنا درجة الحرارة المتوسطة في كل يوم واستهلاك المدينة للمياه في تلك الأيام فكانت البيانات كالتالي:

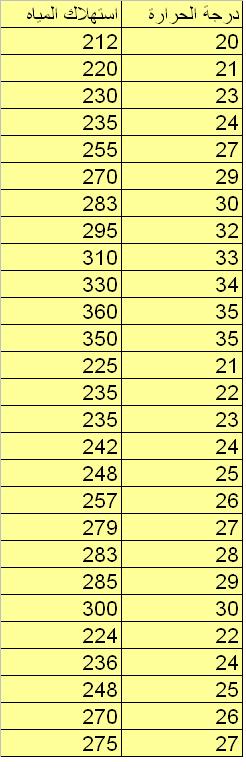بإمكاننا أن نلاحظ ارتفاعا في استهلاك المياه عند ارتفاع درجة الحرارة وهذا أمر متوقع. ولكننا نريد أن نتأكد من ذلك إحصائيا وأن نصل إلى نموذجا رياضيا يمكننا من توقع حجم الاستهلاك عند أي درجة حرارة فمثلا قد نتساءل ما هو حجم الاستهلاك لو وصلت درجة الحرارة إلى 39 درجة مئوية.

برسم العلاقة بين المتغيرين قد تبين لنا هذه العلاقة والتي يمكننا أن نتأكد من قوتها باستخدام معامل الارتباط.

معامل الارتباط =0.97

كل هذا يشير إلى علاقة طردية قوية. ولكن حتى الآن ليس لدينا معادلة رياضية تبين لنا حجم الاستهلاك عند درجة حرارة 20 أو درجة حراة 40 درجة مئوية. نحن بحاجة لإجراء تحليل الانحدار.

نستخدم في ذلك برنامج إكسل. اختر قائمة الأدوات   Tools ثم اختر تحليل البيانات Data   Analysis

بعد ذلك يظهر لنا نافذة بها عدة اختيارات فنختار منها الانحدار Regression

تظهر لنا النافذة الآتية والتي نحدد فيها مكان تسجيل بيانات المتغير التابع (استهلاك المياه) والمتغير المستقل (درجة الحرارة) وقد نضع علامة بجوار Labels إذا كنا قد كتبنا عنوانا لكل عمود مثلما فعلنا في البيانات أعلاه فكتبنا درجة الحرارة واستهلاك المياه في أعلى العمودين. بعد ذلك يمكننا ان نضغط OK

وبذلك نحصل على النتيجة في صفحة منفصلة كالتالي:

نتيجة تحليل الانحدار في إكسل تحتوي على أرقام كثيرة ولكن ذلك لا ينبغني أن يصيبك بالذعر من هذا التحليل فهناك أرقام محدودة نريد التعرف عليها وهي التي قد غطيت بخلفية صفراء. ولمزيد من الوضوح فإن هذه الأرقام نعرضها منفصلة كالتالي

ما معنى هذه البيانات؟

R Square وهي رقم يتراوح بين صفر والواحد الصحيح وهذا الرقم يبين نسبة التغير في استهلاك المياه التي يمكننا توضيحه من خلال هذه المعادلة (يأتي بيانها لاحقا). أي ببساطة هو مؤشر لمدى توضيح تحليل الانحدار لقيمة المتغير الذي نحاول التنبؤ به وهو في هذه الحالة استهلاك المياه. في حالتنا هذه فإن هذا الرقم R Square يساوي o.94 وهو رقم يقترب جدا من الواحد الصحيح مما يعني أن نموذج تحليل الانحدار قوي جدا ويمكننا من حساب قيمة استهلاك المياه بشكل يقترب كثيرا من الصحة. أما لو كانت قيمة هذا الرقم هي 0.3 فإننا يجب علينا إهمال المعادلة التي حصلنا من هذا التحليل والبحث مرة أخرى عن العوامل المؤثرة في استهلاك المياه.

Intercept هو قيمة الثابت ث في المعادلة ص= ث + أ س  والتي تعني في حالتنا

استهلاك المياه = ث + أ x درجة الحرارة

وبالتالي فإن ث= 34.42 ولذلك فإن استهلاك المياه = 34.42  + أ x درجة الحرارة

Coefficient المعاملات والتي تبين قيمة التقاطع مع المحور الرأسي ومعاملات المتغيرات فمثلا قيمة التقاطع مع المحور الرأسي هي 34.42 وقيمة معامل درجة الحرارة هو 8.67

وبالتالي فإن النموذج الرياضي (المعادلة الرياضية) التي حصلنا عليها هي كالتالي:

استهلاك المياه = 34.42  + 8.67  x  درجة الحرارة

P value هي قيمة تظهر إن كان العامل المقابل لها في نفس الصف هو عامل مؤثر فعلا أم لا. في هذه الحالة لدينا عامل واحد وهو درجة الحرارة والتي يقابلها P Value بقيمة  3.98E-17

وهو يعني 0.0000000000000000398

هل هذه القيمة مقبولة أم لا؟ إذا كان P Value أقل من 0.05 فإن العامل المقابل لها (درجة الحرارة في هذا المثال) هو عامل مؤثر في المتغير الذي نحاول دراسة تغيره (استهلاك المياه) وبالتالي فمن الواضح أن درجة الحرارة هي عامل مؤثر فعلا في استهلاك المياه. وقد تعتبر العامل مؤثرا حتى قيمة P Value تساوي 0.1 ولكن إن زادت عن 0.1  فإن هذا العامل يجب استبعاده من النموذج فهو غير مؤثر.

هل درجة الحرارة تؤثر في استهلاك المياه؟

ليس معنى أننا توصلنا إلى علاقة مقبولة إحصائيا بعد دراسة R Square و P Value أن س تسبب تغير ص ولكننا توصلنا إلى علاقة المصاحبة بين س وص أي أن تغير استهلاك المياه يصاحب تغير درجة الحرارة. أي أنه كما قلنا في دراسة العلاقة بين متغيرين عن طريق منحنى الانتشار scatter diagram ومعامل الارتباط Correlation فإننا ندرس وجود مصاحبة بين المتغيرين أو العلاقة بينهما ولكننا لا نستطيع لمجرد وجود علاقة أن نقول أن هذا يتسبب في حدوث ذاك. فمثلا لو درسنا العلاقة بين استهلاك الكهرباء واستهلاك المياه عن طريق تحليل الانحدار فقد نصل لنموذجا مقبولا للعلاقة بينهما ولكن ذلك لا يعني إطلاقا أن زيادة استهلاك الكهرباء تؤدي لزيادة استهلاك المياه ولكننا قد نقول أن كلا منهما يزيد مع زيادة درجة الحرارة نتيجة لتشغيل مكيفات الهواء وزيادة الحاجة للاستحمام بالماء.

والخلاصة أننا لكي نقول أن شيئا ما يتسبب في حدوث آخر فلابد لنا من فهم لطبيعة هذه المتغيرات ودعم قولنا بدراسة أو تحليل منطقي. ففي مثالنا هذا يمكن أن نتوقع علاقة السببية هذه لأن ارتفاع درجة الحرارة فعلا يؤدي إلى زيادة استخدام الناس للمياه في الاستحمام والشرب. ولكن لابد من دعم ذلك بعمل استبيان مثلا لأسباب زيادة استهلاك المياه عند ارتفاع درجة الحرارة.

ما معنى هذه المعادلة؟

توصلنا إلى هذه المعادلة فما معناها؟

استهلاك المياه = 34.42  + 8.67  x  درجة الحرارة

إن هذه المعادلة تعني أن زيادة درجة الحرارة بدرجة واحدة مئوية تعني زيادة استهلاك المياه بـ 8.67. وتعني كذلك أن استهلاك المياه عند درجة حرارة صفر هي 34.42.

ويمكننا استخدام المعادلة للتنبؤ بقيمة استهلاك المياه عند درجة حرارة 40 درجة مئوية

استهلاك المياه = 34.42  +  x    8.67   درجة مئوية   40    =  381

ويمكننا توقع استهلاك المياه عند درجة حرارة 18 درجة مئوية بـ 190

هذه مقدمة لتحليل الانحدار الخطي البسيط. في المقالات التالية إن شاء الله نتعرف بشكل أكثر عمقا وأكثر دقة على هذا التحليل ونتعرف كذلك على تحليل الانحدار المتعدد والذي يربط متغيرا بعوامل عديدة.

مقالات ذات صلة:

الانحدار الخطي المتعدد .. Multiple regression

تحليل الانحدار – دراسة البواقي

معامل الارتباط .. Correlation

مصفوفة النقاط

البرمجة الخطية

التعامل مع البيانات

من مراجع الموضوع:

Lean Six Sigma Pocket ToolBook, M. George at al., MCGrawHill, 2005

Applied Statistical Methods, W. Carlson and B. Thorne, Prentice Hall, 1997

Statistics for Managers, Levine et al., Prentice Hall, 1999

مواقع ذات صلة:

الانحدار الخطي البسيط

Regression Analysis 1 – Video

Regression Analysis 2 – Video

الإعلان